Present Value of an Annuity Explanation & How to Determine
The interest rate can be based on the current amount being obtained through other investments, the corporate cost of capital, or some other measure. To adapt your calculator to an annuity due, you must toggle the payment setting from END to BGN. The payment setting is found on the second shelf above the [latex]PMT[/latex] key (because it is related to the [latex]PMT[/latex]!). The calculator has a large LCD screen at the top which is displaying the number “0.”. Below the screen, there is a keypad with numerous buttons divided into several rows.
Annuity Table: Overview, Examples, and Formulas
However, external economic factors, such as inflation, can adversely affect the future value of the asset by eroding its value. An annuity is a series of payments that occur at the same intervals and in the same amounts. An example of an annuity is a series of payments from the buyer of an asset to the seller, where the buyer promises to make a series of regular payments.
Continuous Compounding (m ⇒ ∞)
For example, a court settlement might entitle the recipient to $2,000 per month for 30 years, but the receiving party may be uncomfortable getting paid over time and request a cash settlement. The equivalent value would then be determined by using the present value of annuity formula. The result will be a present value cash settlement that will be less than the sum total of all the future payments because of discounting (time value of money). If you don’t have access to an electronic financial calculator or software, an easy way to calculate present value amounts is to use present value tables (PV tables). PV tables cannot provide the same level of accuracy as financial calculators or computer software because they use factors that are rounded off to fewer decimal places.
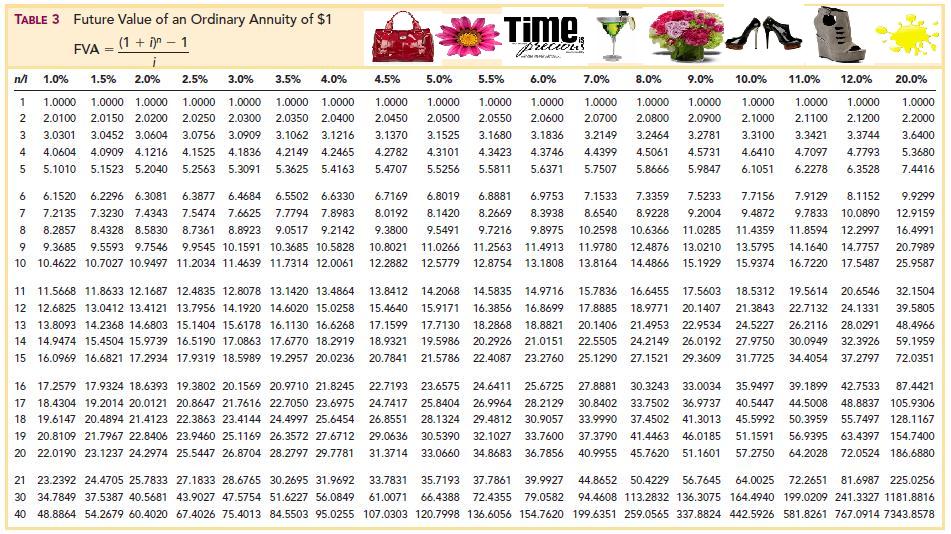
- Therefore, the future value of your annuity due with $1,000 annual payments at a 5 percent interest rate for five years would be about $5,801.91.
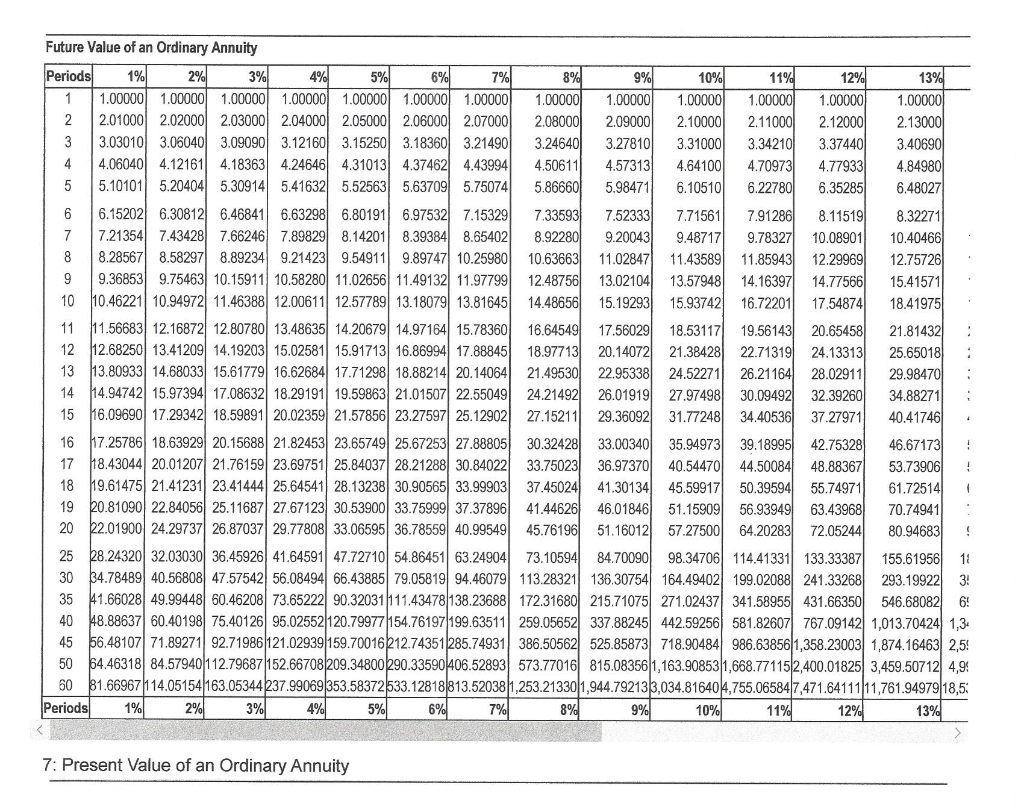
- An annuity table provides a factor, based on time, and a discount rate (interest rate) by which an annuity payment can be multiplied to determine its present value.
- While we strive to provide a wide range of offers, Bankrate does not include information about every financial or credit product or service.
- Because of their widespread use, we will use present value tables for solving our examples.
AccountingTools
Such calculations and their results can add confidence to your financial planning and investment decision-making. Calculating the present value of an annuity can help you determine whether taking a lump sum or opting for future annuity payments spread out over many years will be more beneficial to your financial needs or goals. A discount rate directly affects the value of an annuity and how much money you receive from a purchasing company.
Our writing and editorial staff are a team of experts holding advanced financial designations and have written for most major financial media publications. Our work has been directly cited by organizations including Entrepreneur, Business Insider, Investopedia, Forbes, CNBC, and many others. At Finance Strategists, we partner with financial experts to ensure the accuracy of our financial content. For information pertaining to the registration status of 11 Financial, please contact the state securities regulators for those states in which 11 Financial maintains a registration filing.
The discount rate is a key factor in calculating the present value of an annuity. The discount rate is an assumed rate of return or interest rate that is used to determine the present value of future payments. To determine an individual cash flow, or annuity factor, by using this table, you would look across the top row for the number of periods and down the left side for the interest (or discount) rate.
The reason the values are higher is that payments made at the beginning of the period have more time to earn interest. For example, if the $1,000 was invested on January 1 rather than January 31, it would have an additional month to grow. In contrast to the FV calculation, PV calculation tells you how much money would be required now to produce a series of payments in the future, again assuming a set interest rate. The first column (n) refers to the number of recurring identical payments (or periods) in an annuity. The other columns contain the factors for the interest rate (i) specified in the column heading.
The difference affects value because annuities due have a longer amount of time to earn interest. You can calculate the present or future value for an ordinary annuity or an annuity due using the formulas shown below. There are several ways to measure the cost of making such payments or what they’re ultimately worth. Read on to learn how to calculate the present value (PV) or future value (FV) of an annuity.
It also means that receiving $100 one year from now is less valuable than receiving that same $100 today. In other words, the $100 received one year from now has a present value that is smaller than $100. The table simplifies this calculation by telling you the present value interest factor, accounting for how your interest rate compounds your initial payment over a number of payment periods.
The term “present value” refers to an individual cash flow at one point in time, whereas the term “annuity” is used more generally to refer to a series of cash flows. The present value of an annuity is a calculation used to determine the current worth or cost of a fixed stream of future payments. In contrast, the annuity student loan interest factor is used to calculate how much money must be invested at a given rate of return over a certain period for it to accumulate to a specific sum in the future. Our focus throughout this topic will be on ordinary annuities—streams of equal cash amounts that are received or paid at the end of future periods.
